Reakcja tlenku węgla(II) z parą wodną przebiega zgodnie z równaniem:
CO(g) + H₂O(g) ⇌ H₂(g) + CO₂(g)
W temperaturze T stężeniowa stała równowagi tej reakcji jest równa 2,0.
W zamkniętym reaktorze o stałej pojemności znajdowało się 0.8 mola tlenku węgla(II), 0.8 mola pary wodnej, 0.4 mola wodoru i 0.4 mola tlenku węgla(IV). Mieszaninę utrzymywano temperaturze T aż do osiągnięcia stanu równowagi dynamicznej przez układ.
Oblicz liczbę moli każdej substancji znajdującej się w reaktorze po ustaleniu się stanu równowagi opisanej reakcji.

Zadanie jest bardzo podobne do tego z ostatniego artykułu, różnica polega na tym, że już na początku reakcji w reaktorze znajdują się nie tylko substraty, ale też produkty. Na potrzeby obliczeń tak jak w poprzednim zadaniu, możemy założyć, że objętości jest tyle, że liczba moli reagenta jest równa stężeniu molowemu tego reagenta. Opiszmy stan początkowy reackji:

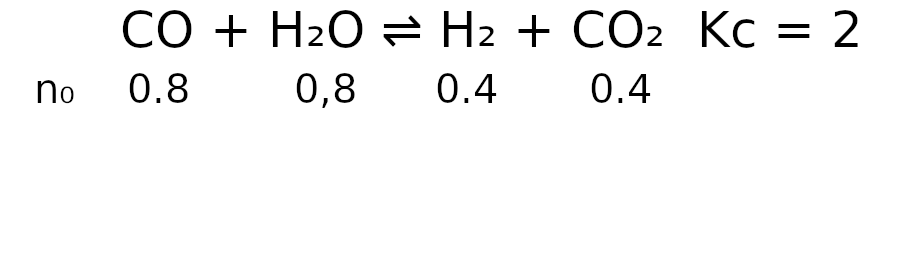
Sytuacja jest zgoła inna niż ostatnio. Wcześniej mieliśmy tylko substraty, co tym samym wskazywało nam, po której stronie reakcji będzie przybywało materii a po której uchodziło. Na potrzeby takich sytuacji możemy obliczyć współczynnik Q. Jego wartość oblicza się bardzo prosto. Należy pomnożyć przez siebie produkty i podzielić je przez iloczyn substratów. Wzór jest jest taki sam jak na obliczenie stałej:

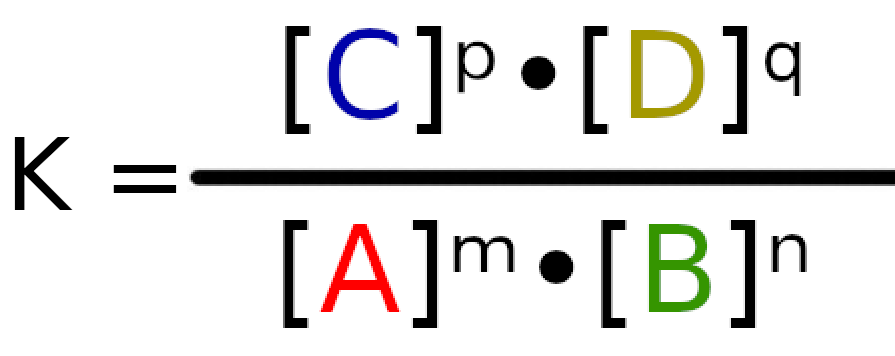
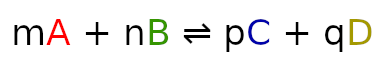
ale w tym wypadku pod K podstawiamy Q i obliczamy stężenia na początku reakcji.

Q = ¹⁄₄ 

Co dalej robić z tym faktem? Współczynnik Q przyrównujemy do stałej równowagi K. Jeżeli:

Q > K substratów będzie przybywało, produktów ubywało
Q < K produktów będzie przybywało, substratów ubywało
Q = K stan początkowy reakcji jest już stanem równowagi i na tym można by zakończyć wszelkie obliczenia i wypisać stężenie końcowe

Warto się zatrzymać i rozważyć powyższe stany. ***

W tym przypadku spotykamy się z wariantem gdzie Q < K, więc zapiszmy dane w następujący sposób:

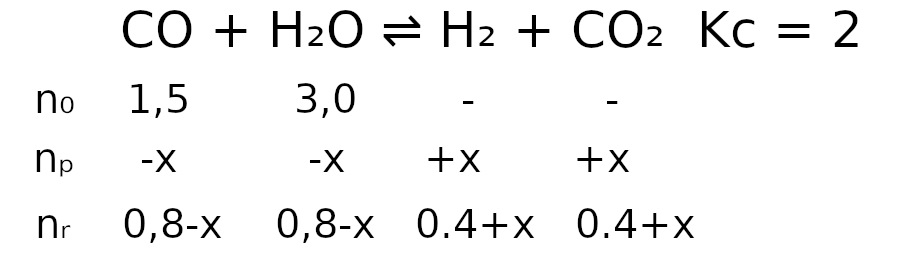
Podstawmy dane do wzoru i możemy zacząć zabierać się za wyprowadzanie wzoru.

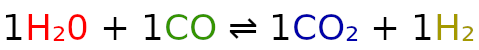
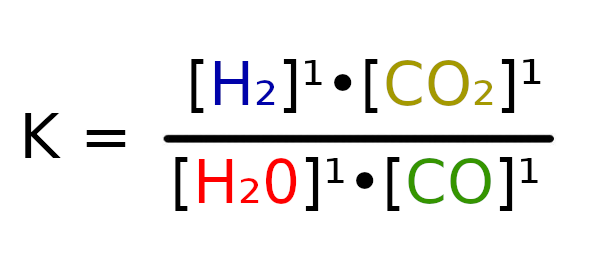
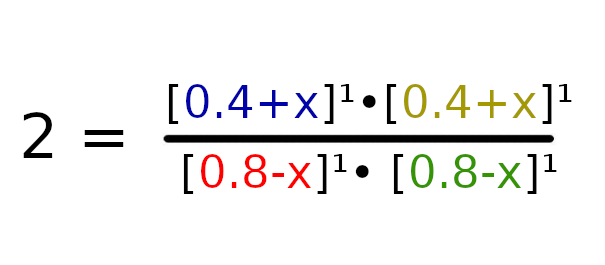
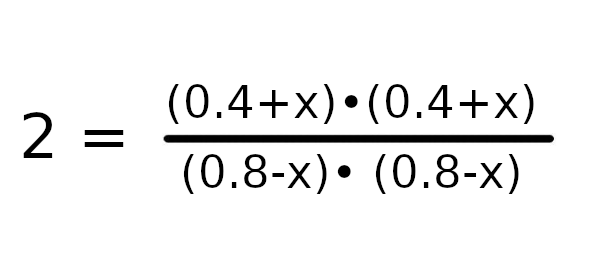
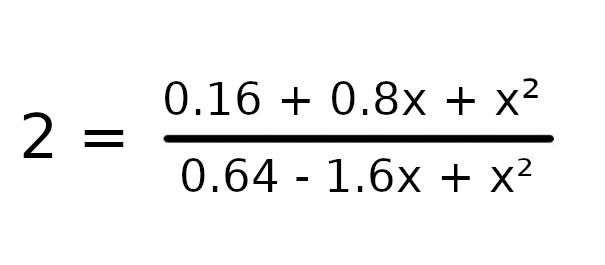
Przemnóżmy obustronnie równanie przez wartość 0.64 – 1.6x + x w celu usunięcia mianownika.

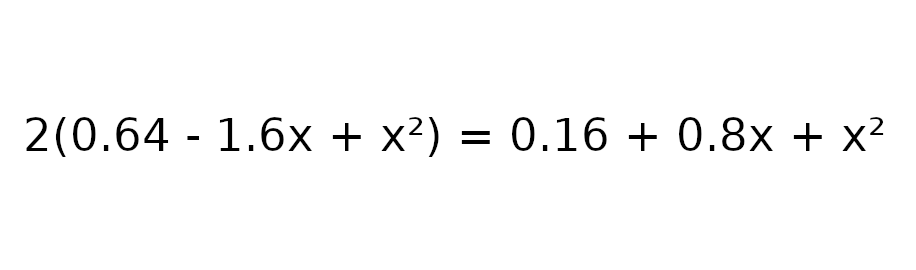
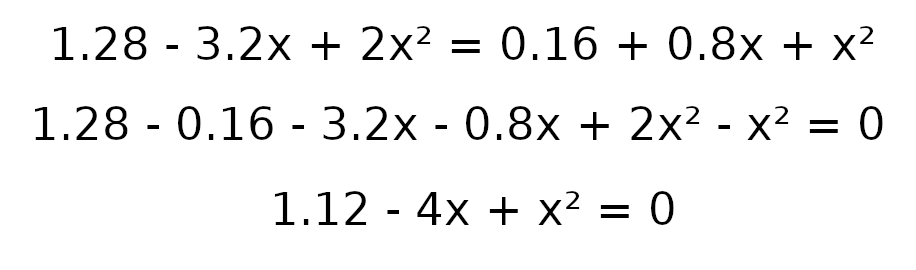
Następnie wprowadźmy dane do obliczenia delty

a = 1
b = -4
c = 1.12

Wzór na deltę Δ = b² – 4ac.

Δ = (-4)² – 4 • 1 • 1.12
Δ = 16 – 4.48
Δ = 11.52
√Δ = ~3.39

Δ > 0, więc korzystamy z 2 wzorów na miejsce zerowe

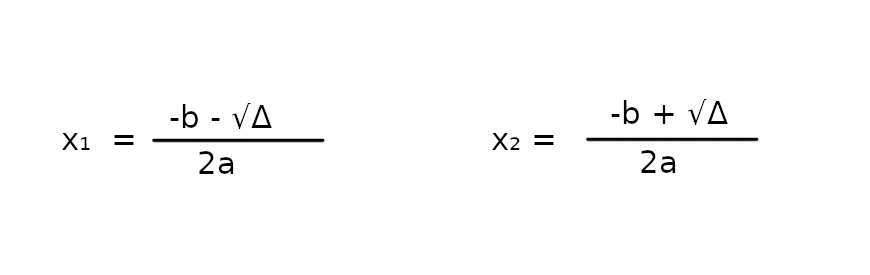
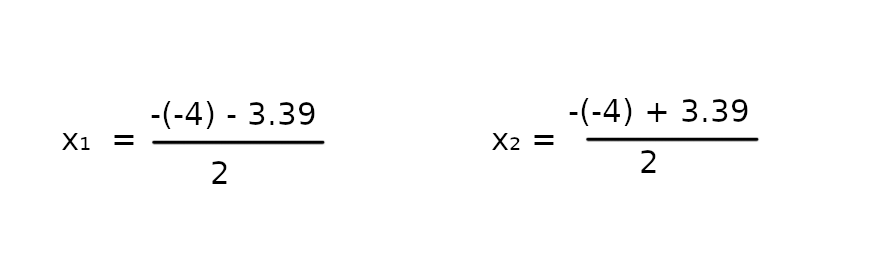
x₁ = ~0.31
x₂ = ~3,70

Odrzucamy x₂, ponieważ odejmując tę wartość od 0.8 wynik stężenie wyszedłby ujemny, więc przyjmujemy, że wynik x₁ jest poprawny.

x = 0.31
CO = 0.8 – 0.31 = 0.49
H₂O = 0.8 – 0.31 = 0.49
H₂ = 0.4 + 0.31 = 0.71
CO₂ = 0.4 + 0.31 = 0.71

Zgodnie z naszym założeniem o objętości w reaktorze te stężenia są również ilością moli. Tak więc podane wyniki są już gotową odpowiedzią do zadania.